Using advanced data analysis techniques, or even just reading about them, we often come across the term "multidimensional technique". Are there really many dimensions in the world? Traditionally, there are only three dimensions: width, height and depth. The fourth, fifth, sixth dimension - it sounds like a science fiction film idea!
How to imagine multidimensionality?
Before we go into space, where we will be transformed into the fourth dimension, let us go down to earth for a moment and consider a simple example. We will start with a one-dimensional graphic representation of two points. Points A and B are given. The distance between them is two units. The position of the points on the x-axis is shown in the following diagram.

Figure 1. One-dimensional graphic representation of the position of points
Imagine that there is a third point C, which is located at a distance of approximately 3 units from point A and at a distance of approximately 3 units from point B at the same time. If we limit ourselves to only one axis, it is impossible to represent the position of point C. If the AC distance is to be 3, we would have to set it either to 5 or to -1 on the x-axis. However, in none of these cases will the BC distance be 3. The only way to do this is to add a second axis - the y-axis, to create a two-dimensional space instead of a one-dimensional one.
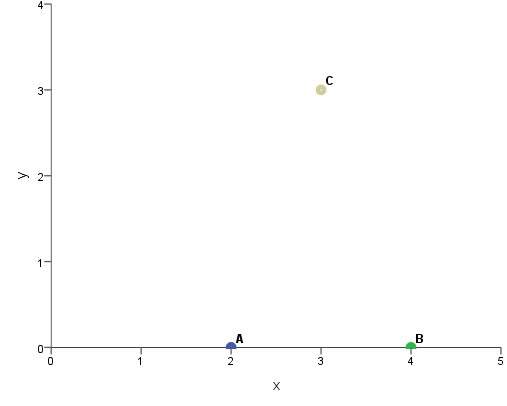
Figure 2. Two-dimensional graphic representation of the position of points
It's pretty simple so far. Then let's add one more point. The distances of the new point D from points A, B and C are shown in the table below.
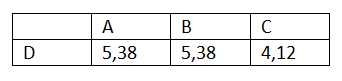
Table 1. Distances of point D from points A, B and C
Is a simple two-dimensional coordinate system enough for us? It seems that it is not. A point which is distant by the given values from other points must be either "deep" in the chart or closer to us. In order to add such a point, we need to draw another dimension to the graph. Of course, it is not possible to draw a three-dimensional space on a flat sheet of paper to accurately represent all distances between points. The following presentation may be helpful to imagine the arrangement of points, but in fact it would be best to build a three-dimensional model. We can see, therefore, that already three dimensions can cause us some difficulties. But the fun is just beginning!
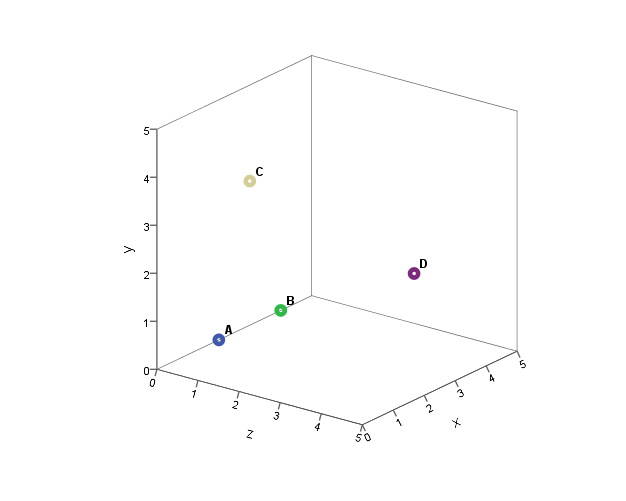
Figure 3. Three-dimensional graphic representation of the position of points
From a mathematical point of view, there is no reason for us to stop at three dimensions. After all, we can introduce new points into our space. Of course, some points can be located in space using the existing dimensions, but sometimes it will be necessary to introduce a new dimension. Unfortunately, we will not present it graphically any more, but we can, for example, calculate the coordinates of a given point on the fourth, sixth or even twelfth dimension....
This can also happen when social or consumer research data is analyzed. Suppose we want to know which brands, in the eyes of consumers, are most similar to each other and which are very different from each other. By introducing consumer assessments into the analysis, we may not even realize that the analytical procedure must calculate a matrix of distances between brands on the basis of these data. If we require the program to show us the similarities between the brands in graphic form, we face a difficult problem: how to show in two dimensions something that in reality is multidimensional? In order to cope with this, it will be necessary to reduce the multidimensionality.
The idea of reducing multidimensionality
Until now, we've been making our lives more difficult and now we're going to think about how to make them easier for ourselves. Instead of adding more dimensions, we are now going to reduce them, i.e. reduce the multidimensional space to a smaller number of dimensions.
We already agree that the position of a point can be determined on many different dimensions. However, since it is very difficult to imagine points lying in a multidimensional space, we would like to reduce these points to three, or preferably two, dimensions. Reducing the number of dimensions is possible by projecting points on a plane. Let us return to the example that was discussed earlier. I can ignore the existence of the third dimension and project a point D on the plane defined by the xy coordinate system.
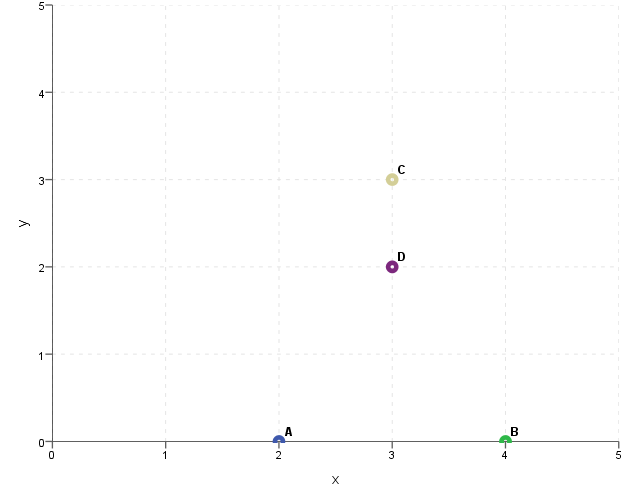
Figure 4. Projecting the position of points on the plane defined by the Xy-axis
The result is a certain distortion - point D looks as if it was close to the other points, although we know that its actual distance was greater. Then we can make another projection. Let's try to use the z-axis and y-axis.

Figure 5. Projecting the position of points on the plane defined by the ZY-axis
Now you can see that point D is far from the others. However, there is a problem with points A and B, which "overlap" and look as if they are located in the same place. Of course, this is due to the fact that we ignored the existence of the dimension x, which is responsible for the differentiation of A and B points. There is also a third possibility - you can use x-axis and z-axis. Which distances will then be well represented and which will seem smaller than they really are?
I leave it up to you to answer that question.
So far, the projection of points on the plane does not seem satisfactory. However, let us think about the fact that the plane on which we project points does not have to be parallel to the existing axes. We can freely "set" such a plane in our cube. Finding a suitable plane will allow for a good reflection of the actual location of points in space. It will never be perfect, but you can do your best to keep the falsification as small as possible.
The following conclusion can be drawn from the previous considerations: if we want to simplify our lives and reduce the number of dimensions, we must, unfortunately, agree to the loss of some information about the diversity of objects. However, there is a good chance that such a move will pay off. With a skillful selection of the plane, the loss of information will be small, and the benefits of reducing the dimensions can be very large.
Which dimension is important and which is not?
We will now consider whether we can say that one dimension is more important than another and on what basis we can say it. Let us look at the following two-dimensional coordinate system and the points scattered in this system.
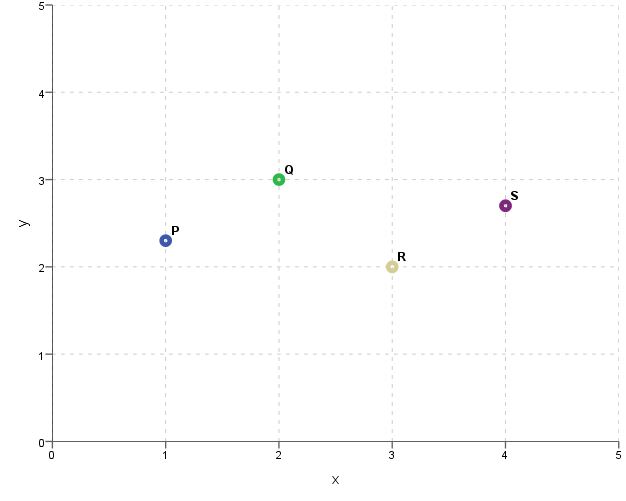
Figure 6. Representation of the position of P, Q, R and S points in a two-dimensional space
If we were to reduce these points to a single dimension using the x-axis or the y-axis, which one would it be better to choose? The graph below shows the result of projecting points on the x-axis.

Figure 7. The result of the projection of points P, Q, R and S on the X-axis
Let us compare this with the result of projecting points on the y-axis.

Figure 8. Result of the projection of points P, Q, R and S on the Y-axis
Points are more strongly differentiated in the first dimension (for which the x-axis is responsible). By removing it, we end up with a very large loss of information. The second dimension (represented by the y-axis) represents some additional value, but is not essential. When we remove it, we lose some information, but the loss is not that big. If it were necessary to remove one of these two dimensions, we would certainly prefer to remove the dimension represented by the y-axis.
By analogy, let us now think of a multidimensional space. Most often we will want to reduce all points to two dimensions. In order to lose as little information as possible during this period, we will look for two dimensions that are responsible for the greatest scattering of points. To find such dimensions we can use, among others, the correspondence analysis.
Let us take a moment to summarize what I have written about. First of all, however, you will have to look at science fiction movies with a slightly more positive eye. The existence of many dimensions is not a meaningless theory. Secondly, because of the (unfortunately!) limitations of the human mind, we are forced to help ourselves in the analysis of data by reducing multidimensional phenomena to two dimensions. At the same time, we agree to lose some of our information. Fortunately, because not all dimensions are equally important, we can reject those that would not provide much information for analysis anyway.