Measures of asymmetry and concentration of the distribution of a variable
Kurtosis and skewness are measures of asymmetry that describe such properties as the shape and asymmetry of the distribution under analysis. They provide us with information on how the values of the variables deviate when compared to the mean value. Thus, they allow us to answer the question of whether the mean is in the center of the distribution (and therefore close to the median), how individual observations are dispersed around this mean, and how extreme are outlying observations.
What is skewness and what does it tell us?
Skewness is a statistic that makes it possible to compare the distribution of the analyzed variable with a hypothetical normal distribution. It indicates the discrepancy between the mean value and the center of a given distribution. In turn, as is well known, the mean is characterized by its lack of robustness in the presence of extreme values. Therefore, if during the analysis of the distribution of a given variable we notice the presence of abnormally small or large values, we can conclude that the average has been "dragged" by these extreme values to the right or left. For example, in a situation with unusually small values, the average is "dragged" to the left side, When viewed on a graph, you will observe an elongated left tail of the distribution, or the occurrence of a left-skewed distribution.
How to interpret the coefficient of skewness (asymmetry)?
The skewness coefficient As can take negative values, equal zero, and take positive values. Depending on the value of the coefficient, it can be interpreted as follows:
- As < 0 – Left-skewness
- Mo > Me >

- extended left tail of the distribution
- As = 0 – Symmetric distribution
- Mo = Me =

- As > 0 – Right-skewness
- Mo < Me <

- extended right tail of the distribution
Mo – mode
Me – median
![]() - mean
- mean

Figure 1. Types of distributions by value of skewness coefficient
What is kurtosis and what does it tell us?
We also use kurtosis to compare the distribution of the analyzed variable with a hypothetical normal distribution, in which the dispersion of observations around the mean is relatively uniform and there are no extreme outliers. Depending on the value of kurtosis, the plotted distribution can have a "fatter" or "thinner” tail, which is influenced by the intensity of extreme values.
Based on its value, we can distinguish three types of distributions:
- leptokurtic (K>0) - the distribution has a fatter tail, i.e., the intensity of extreme values is higher than in a normal distribution.
- mesocurtic (K=0) - the distribution is close to normal.
- platykurtic (K<0) - the distribution has a thinner tail than the normal distribution, i.e., the intensity of extreme values is lower than in the normal distribution.

Figure 2. Types of distributions by value of kurtosis
Let's look at an example analysis of the distribution of three variables such as the age of a customer, his expenditure, and the price of a certain product. Below are basic descriptive statistics relevant to this analysis generated using PS IMAGO PRO.
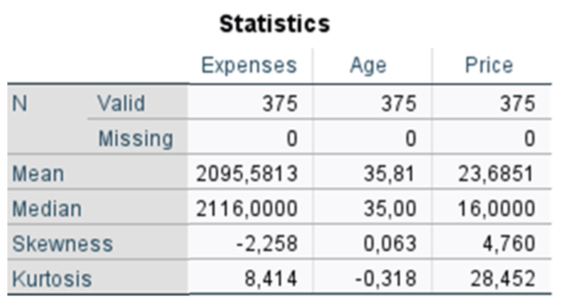
Table 1. Selected descriptive statistics for the analyzed variables
For the expenditure variable, it can be inferred that the distribution will be left-skewed (skewness value < 0) and will have a fat tail given the value of kurtosis.
In the case of the age variable, both the value of skewness and kurtosis are close to 0, which indicates that the distribution of this variable is similar to a normal distribution.
Based on the value of skewness for the price variable, it can be concluded that its distribution will be characterized by strong left asymmetry and greater intensity of extreme values than in a normal distribution, as indicated by the high value of kurtosis.
As we have already analyzed the values of the statistics in the table, it is still worth looking at the following visualizations (histograms) for the distribution of the analyzed variables, enriched with the normal distribution curve. Often it is on the basis of these graphs generated using PS IMAGO PRO that we can quickly detect some relationships and features of the distributions of the analyzed variables.
On the histogram of the expenditure variable, it can be observed that the left tail of the distribution is spectrally elongated, indicating left-skewness. In addition, note that observations more often take on extreme values than would result from a normal distribution (see the left-hand fat tail of the distribution).

Figure 3. Histogram of the expenditure variable
In the case of the age variable, as we noted from the values of skewness and kurtosis, the distribution can be considered close to a normal distribution. In the graph, there is no noticeable asymmetry of the distribution (none of its tails are excessively stretched) or excessive intensity of outlying observations as in the case of the distribution of the expenditure variable.

Figure 4. Histogram of the age variable
The last histogram shows the distribution of the price variable. At first glance, two properties of the distribution of this variable can be observed. The first is the visibly elongated right tail of the distribution, indicating its strong rightward skewness. Second, we can see that the observations are much more likely to take extreme values (see the right-hand fat tail of the distribution) than we would expect when comparing to a normal distribution.

Figure 5. Histogram of the price variable
To summarize, skewness and kurtosis are measures that the analyst uses when looking for answers to the question of how individual observations are dispersed around the mean, how extreme are outlying observations, and whether the mean is really in the center of the analyzed distribution.
At the beginning of working with data, it is particularly useful to present the distributions of the analyzed variables in the form of histograms which allows one to easily and quickly grasp the most important properties, such as the discussed asymmetry or the way observations are concentrated.