The Gini index is a measure of the concentration of a variable's distribution. In statistics it is commonly used to describe the concentration (unevenness) of the distribution of a random variable, while its most popular use in economics is as a measure of the degree of income inequality.
Gini index as a measure of variation in qualitative variables
The Gini index is also used as a measure of variation for qualitative, categorical variables. We encounter categorical data in many types of analysis, very often in scientific fields such as sociology, economics or biostatistics. One of the measures used to analyse variation is precisely the Gini index expressed by the formula:
where:
k - number of categories of the variable,
- probability of belonging to a given category.
The value of the Gini index indicates how much variability there is in the qualitative variable under study. It can be compared to the variance and standard deviation calculated for quantitative variables.
The Gini index describing the concentration of the distribution of qualitative variables can take values from zero, while the upper limit is not strictly defined. The maximum value that the Gini index can take depends on the number of categories of the variable. If a variable had two categories, the maximum variability would be 0.5, whereas if there were four categories, each category would contain 25% of the observations, so the Gini index would be 0.75. Note that the number of categories only affects the value of the maximum variability that can be achieved for a given variable. The minimum value is always zero and represents the absence of variability giving us certainty in decision-making. This is the situation when all observations belong to only one category of the variable. This means that if we wanted to predict from such a distribution of a variable whether an observation belongs to a particular category, we would be right 100% of the time.
To explain, we will use the example of the variable gender having two categories - female and male. When analysing the variability, we will use the percentage of people in each category.
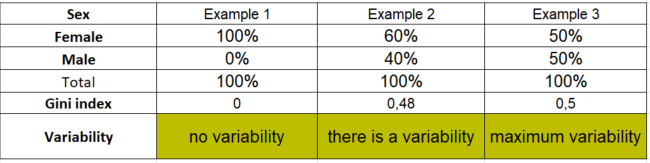
Table 1. Analysis of variation for a variable with two categories
Table 1 shows three different cases of the distribution of the gender variable. In the first case (Example 1), all the people taking part in the survey are women. Using the above formula, we calculate the Gini coefficient: 
. The Gini coefficient will take on a value of 0, which means that in this example the trait shows a lack of variability, i.e., certainty in decision-making.
Looking at the distribution of the gender variable in the second example, we notice that 60% of the respondents are female and 40% are male resulting in moderate variability. If we wanted to predict from this distribution whether a respondent is female, we would be wrong 40% of the time. Calculating the Gini coefficient for such a distribution of the nominal variable, we obtain: 
.
The last column of the table (Example 3) shows the distribution of the variable in which we have the maximum variability. As already mentioned, the minimum value of the Gini index is zero, which means no variability, while the maximum that can be reached depends on the number of categories of the variable. Thus, in the case of gender, the maximum variability will be reached when there are 50% of observations for each category. The Gini coefficient will therefore be 0.5 and this is the maximum variability that can be achieved for a variable with two categories.
Similarly, if we were to analyse a variable with four categories, the maximum variability (0.75) will be reached when each category contains 25% of the observations.
Gini index for qualitative variables in PS IMAGO PRO
Let us look at an example of the use of the Gini coefficient available in the Data Audit procedure in PS IMAGO PRO. The procedure calculates the value of the Gini index and what percentage of the maximum value of the Gini index is its calculated value for the analysed variable (Gini versus maximum value - Table 3). Keep in mind that the maximum value of the Gini index is variable and depends on the number of categories of the analysed characteristic.
Let us look at the distribution of the variable presenting the completed field of study of the people taking part in a certain survey.
Table 2. Distribution of the variable field of study
The variable has four categories, so we can conclude that the maximum value of the Gini coefficient will be 0.75 
. Recall - the minimum value of the index will be 0 in the case of no variability, i.e., when all respondents state that they graduated from the Faculty of Law.
The table below shows the value of the Gini index and the Gini compared to the maximum value - that is, the percentage of maximum variability possible for this variable.
Table 3. Gini (value) and Gini (percentage) compared
to maximum value for the variable field of study
The Gini index value for the variable representing the field of study is 0.72775, indicating high variability. Given that the maximum possible variability is 0.75, the Gini compared to the maximum value is 97.03% - meaning that the variability of the field of study represents 97.03% of the maximum variability that this variable can take.
Summarising the above examples, we can see that the Gini index, in addition to common applications such as measuring income inequality, can be used to analyse the variation of variables in categorical data found in many scientific and business fields.